Referentie-intervallen
Inhoud
What's in a name?
Het feit dat RI als normaal-abnormaal meter worden gebruikt, is gedeeltelijk toe te schrijven aan misbegrepen terminologie. De termen normaalwaarden en normaalwaardenbereik hebben niets met pathologie of gezondheid te maken maar verwijzen naar de statistische verdeling die vaak van toepassing is op bio-analytische parameters: de normaal- of Gausscurve. Omwille van deze begripsverwarring en omdat niet alle parameters normaal (of juister lognormaal) verdeeld zijn, spreken we liever van referentie-intervallen.
Hoe worden RI berekend
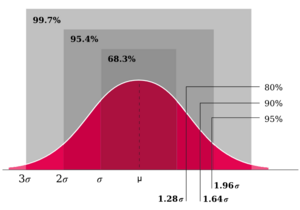
RI worden opgesteld rond de het gemiddelde van de referentiepopulatie gebruik makend van de normaaldistributie zodat 95% binnen de grenzen valt, 2.5% onder de lage grens en 2.5% boven de hoge grens ligt. Dit komt (grofweg) neer op:
µ ± 1.96 x σ, afgerond µ ± 2 x σ waarbij µ = populatiegemiddelde en σ = spreiding
Het echte gemiddelde en spreiding van de volledige populatie is echter nooit gekend. Er wordt immers slechts een steekproef genomen van n individuen uit de gezonde populatie. Om hiervoor te compenseren is het correcter om het RI als volgt te berekenen
X ± t(0.975,n-1) x ( (n + 1) / n)1/2 x s waarbij X = steekproefgemiddelde en s = spreiding n = steekproefgrootte t(0.975,n-1)97.5% kwantiel van de Student's t-distributie met n-1 vrijheidsgraden
In werkelijkheid volgen biologische parameters meestal een lognormale verdeling. Wat wil zeggen dat niet de gemeten waarde normaal verdeeld is maar wel het logaritme ervan. De reden hiervoor is de neiging van biologische parameters om even sterk tov het gemiddelde bvb te verdubbelen als te halveren. Met een voorbeeld: als het gemiddelde voor glucose 100 mg/dL bedraagt dan is de kans dat men bij een willekeurig individu 125 mg/dL meet even groot dan men 80 mg/dL meet (maal resp. delen door 1.25). Bovendien kunnen biologische parameters geen negatieve waarde aannemen, terwijl er aan de hoge zijde geen eindige limiet bestaat, wat resulteert in positieve scheefheid.
Om RI volgens het lognormale model te berekenen komt dit praktisch er op neer dat men alle meetwaarden omzet in bvb hun natuurlijk logaritme (ln), vervolgens hiervan gemiddelde en spreiding berekent die men gebruikt in bovenstaande formules. De bekomen grenzen moeten dan uiteraard nog geconverteerd worden naar hun oorspronkelijke schaal dmv het inverse logaritme (elimietwaarde).
Zolang de spreiding van de gemeten waarden klein is tov het gemiddelde is deze scheeftrekking van weinig belang. Men kan berekenen dat zolang deze verhouding <21.3% men het normaalmodel kan hanteren. Een andere vuistregel is dat de grenzen berekend volgens het normaalmodel niet verder dan 2.4 keer uit elkaar mogen liggen. Indien toch het geval dan herberekent men de grenzen beter via het lognormaalmodel.
Variabiliteit
Variabiliteit wordt uitgedrukt in een Coefficient of Variation (CV) wat niets ander is dan de verhouding van de spreiding (σ) tov het gemiddelde (µ).
CV = σ/µ
RI zijn het resultaat van (pre)analytische en biologische variabiliteit.[1] Analytische variabiliteit (CVA) is afhankelijk van de toegepaste methode, de laborant en omgevingsfactoren die schommelingen veroorzaken in instrumentarium en reagentia. Over het algemeen is deze klein (5-10%) en wordt bovendien voor, tijdens en/of na iedere run bewaakt door controlemonsters met een gekende hoeveelheid te analyseren.
Ook pre-analytische factoren zoals manier van staalname, afnamemateriaal, stockage en transport introduceren een niet te onderschatten bron van variatie die in praktijkomstandigheden bovendien veel moeilijker te controleren valt.
Biologische variabiliteit wordt verder opgedeeld in variatie die bestaat binnen de leden van eenzelfde groep (inter-individueel, CVG) en binnen één individu over de tijd heen (intra-individueel, CVI). De CVI wordt bepaald door van enkele (10-20) klinisch gezonde dieren (meerdere rassen, gespreide leeftijden en geslachten) een 14-tal metingen uit te voeren volgens een dagelijks, weekelijks en maandelijks schema. Deze variatie is onafhankelijk van labo, methode en meestal zelfs van ziekte of gezondheid, hoewel CVI voor ziektespecifieke parameters in geval van ziekte groter kan zijn (bvb creatinine igv nierinsufficiëntie)[2]
Tot op heden zijn er slechts een handvol studies die op een bescheiden manier CVI in kaart hebben gebracht, voor slechts enkele parameters, en dan nog enkel bij honden.[3][4][5][6].
Een eerste nut dat men haalt uit kennis van variabiliteit, zijn de stelregels dat voor het opvolgen van een patiënt, maw meetwaarden vergelijken tov elkaar in de tijd (monitoring), de analytische variabiliteit ten hoogste de helft van de intra-individuele mag bedragen[7].
CVA < 1/2 CVI
Wil men louter de individuele waarde vergelijken met het populatie gebaseerde RI dan geldt
CVA < 1/2 (CVI2 + CVG2)1/2
Hoe worden RI opgesteld?
Het de novo opstellen van een RI vereist bemonstering en analyse op een gestandaardiseerde wijze van minstens 120 gezonde individuen na inclusie dmv vooraf opgestelde criteria. Alternatief kan men de data a posteriori vergaren in zoverre men in staat is de inclusiecriteria dan nog te evalueren.[8][9]
Het probleem hiermee is dat er geen algemene definitie voor gezondheid bestaat. Mag men voor het bepalen van een RI voor laat ons zeggen leverwaarden dieren met een allergie insluiten? Is een cryptorch gezond of niet? Ondanks strikte criteria is ook uit eigen ervaring gebleken dat de kans op inclusie van subklinisch zieke individuen zeer reëel is. En rassen: de Cavalier King Charles Spaniels met hun kenmerkende grote thrombocyten: meetellen of niet? In hoeverre heeft geslacht, dracht, lactatie, leeftijd en conditie invloed op de biologische variatie, om nog te zwijgen over dieet, huisvesting,...? 120 Beagles insluiten is ook geen goed idee. Verlost van de rasinvloed gaat tegelijk een groot deel van de biologische variabiliteit waarnaar men juist op zoek is, verloren en bekomt met een RI dat in het beste geval bruikbaar is voor Beagles maar weinig zinvol in praktijkomstandigheden. De bemonstering zelf heeft ook ongetwijfeld effect: afnameplaats en manier van afname, stress, type afnamemateriaal, bewarings -en transportomstandigheden. Hoewel geen aandeel in de biologische variabiliteit, beïnvloeden deze factoren wel de totale variabiliteit bij gezonde dieren in praktijkomstandigheden; insluiten dan maar of toch maar niet? In zoverre men over de tijd en middelen beschikt om een referentiepopulatie samen te stellen, alle relevante factoren uit te zoeken en te bediscussiëren zal men steeds eindigen met een consensus. De ironie is dat hoe meer variabiliteit men insluit hoe groter de kans op ruis; hoe strikter de insluitingscriteria hoe minder gewenste variabiliteit overblijft. Deze techniek is al helemaal problematisch voor exotischere diersoorten of soorten waar staalname weinig evident is.
Een tweede manier voor het opstellen van RI is transferrentie of validatie van reeds bestaande (de novo opgestelde) RI. Hiervoor zijn minder testindividuen nodig (20 of 40) en wordt statistisch nagegaan of de bestaande RI toepasbaar zijn voor de eigen populatie binnen het eigen labo volgens de eigen methode. Desgevallend worden ze alsdusdanig overgenomen.[8] [9]Op het eerste zicht een aantrekkelijk alternatief, blijft de noodzaak van aanvankelijk de novo opgestelde RI waarvan men het studiedesign, gehanteerde criteria en standaarden vaak niet kent. Deze methode wordt ook binnen het labo toegepast wanneer de testmethode of analyseapparatuur ingrijpend verandert. Maar tgv analysedrift bestaat er geen garantie dat de methode van vandaag resultaten produceert die vergelijkbaar zijn met die op het moment van de originele RI-studie. Laat deze techniek de hoofdreden zijn waardoor velen compleet verouderde RI gebruiken van decennia geleden.
De derde methode is de indirecte methode[10] waarbij men alle data van alle patiënten ongeacht ziekte of gezondheid statistisch analyseert. Het gaat hier niet over honderden maar duizenden, tienduizenden of meer waarden. In de redenering dat er geen ziekte bestaat met een prevalentie zelfs maar dicht bij de 50%, moet er zich wel binnen een grote reeks bepalingen een populatie afzonderen rondom een centraal gemiddelde: nl. de gezonde of normale (althans voor de beschouwde parameter) populatie. Hoewel tegen de aanbevelingen in, levert deze brute-force methode verassend genoeg vaak RI op die zo goed als volledig overeenkomen met gepubliceerde RI of RI bekomen via de klassieke de novo techniek. Het is niet onlogisch dat abnormale waarden zich eerder willekeurig gedragen daar waar normale waarden zich rond een gemiddelde organiseren. Bovendien zijn de directe methodes zoals hierboven aangehaald ook niet vrij van hun eigen veronderstellingen.
Index of Individuality
De Index of Individuality (IoI) geeft de verhouding weer van de inter-individuele tov de intra-individuele variabiliteit en wordt als volgt berekend:
CVG / (CVA2 + CVI2)1/2
Parameters met een laag CVI en een hoge CVG hebben aldus een hoge individualiteit. Origineel werd het reciproke voorgesteld maar dan ontstaat de semantische verwarring waarbij parameters die binnen het individu weinig variëren een lage numerieke waarde voor IoI krijgen, terwijl men intuïtief verwacht dat een sterk individu-gebonden variabiliteit samengaat met een hoge IoI.
Uit de IoI werden volgende stelregels opgesteld[11]
| IoI | Besluit |
|---|---|
| <0.7 | De variabiliteit binnen het individu is groter dan die binnen de populatie. Vergelijking van de meetwaarde tov (klassieke) populatie-gebaseerde RI is informatief en zinvol in tegenstelling tot RCV. |
| >1.7 | De variabiliteit binnen het individu is beduidend kleiner dan die binnen de populatie. Vergelijking van de meetwaarde tov (klassieke) populatie-gebaseerde RI is van beperkt nut. De kans is groot dat er veranderingen gemist worden die wel degelijk van medisch belang zijn. Het is beter om RCV te gebruiken om de significantie van schommelingen van opeenvolgende metingen na te gaan. |
Een ander geopperde stelling is dat wanneer een waarde buiten het (populatie) RI valt een tweede meting geen bijkomende informatie verschaft indien de parameter een hoge IoI heeft. Een tweede meting zal immers sowieso dicht bij de eerste liggen. Men heeft een RCV nodig om te beslissen of een afwijking tussen de eerste en de tweede meting significant is. Is de IoI echter laag dan kan men met een herhaalde meting het aantal vals negatieven of positieven merkelijk verlagen.[12]
Reference Change Value
De Reference Change Value (RCV) of kritisch verschil geeft aan hoe sterk een waarde moet wijzigen tussen twee opeenvolgende metingen bij hetzelfde individu om statistisch significant te zijn. De RCV wordt berekend via onderstaande formule:[13]
RCV = Z x (2 x (CVA2 + CVI2)1/2 waarbij Z = Z-score (95% probabiliteit (p<0.05) Z = 1.96)
Of het nuttig is de RCV dan wel het klassieke RI te gebruiken hangt af van de IoI zoals hierboven uitgelegd. Aangezien ook de analytische variabiliteit in acht wordt genomen is RCV labo-afhankelijk tenzij CVA2 < 1/2 CVI wat dikwijls het geval is. Dan kan men de berekening afkorten tot:
RCV = Z x 21/2 x CVI
Het homeostatisch punt waarrond een waarde binnen een individu schommelt zal tijdens ziekte verschuiven. Bij de mens blijft ook bij ziekte de mate van schommeling (CVI) echter nagenoeg constant, behalve bij ziektespecifieke merkers (zoals tumormerkers).[2]
Cut-offs
In de humane geneeskunde wordt er vaak ook gewerkt met decision limits of cut-offs: tot daar of van hier wordt die of die diagnose gesteld of wordt zo of zo behandeld, ... klinische beslissingen dus. Om wereldwijd bruikbaar te zijn, moeten deze onafhankelijk zijn van laboratorium en methodologie, wat op zijn beurt gestandaardiseerd calibratiemateriaal vergt. In de diergeneeskunde voorlopig iets om over te dromen. De limieten die men aantreft in de literatuur, aanhaalt op congressen e.d. zijn in zoverre toepasbaar op waarden gemeten in het eigen labo dat men zowel de methodologie waarbij deze limieten gelden als de methodologie van het eigen labo kent, wat helaas zelden het geval is.
Tov een cut-off of (ondergrens of bovengrens van een RI) kan men een reeks berekeningen uitvoeren die de kracht of zwakte van de gekozen cut-off waarde kwanitificeert. Indien we een populatie met T individuen testen en een cut-off X vooropstellen om ziekte te detecteren, kunnen zich volgende mogelijkheden voordoen:
- een individu test positief (>X) en is ook daadwerkelijk aangetast = echt positief (EP)
- een individu test positief (>X) maar is in werkelijkheid gezond = vals positief (VP)
- een individu test negatief (≤X) maar is in werkelijkheid ziek = vals negatief (VN)
- een individu test negatief (≤X) en is ook daadwerkelijk gezond = echt negatief (EN)
of schematisch weergegeven.
| echte uitkomst | ||||
|---|---|---|---|---|
| totaal (T) | ||||
| gemeten uitkomst |
Echt Positief |
Vals Positief |
P' | |
| Vals Negatief |
Echt Negatief |
N' | ||
| totaal (T) | P | N | ||
Hieruit kan men volgende ratio's berekenen:
- True Positive Rate (TPR) of Sensitiviteit = TP / (EP +VN) = EP / P
- Hoeveel van het aantal aangetasten individuen wordt herkend, hoe gevoelig is de test voor de ziekte.
- Specificiteit = EN / (VP + EN) = EN / N
- Hoeveel van het aantal gezonde individuen wordt herkend, in hoeverre verstoren andere ziektes/eigenschappen, hoe specifiek is de test voor de ziekte.
- False Positive Rate (FPR) = VP / (VP + EN) = 1 - Specificiteit
- Hoeveel van de gezonde individuen worden als aangetast beschouwd.
- Accuraatheid = (EP + EN) / T
- Hoeveel individuen worden correct geklassificeerd.
- Positive Predictive Value (PPV) = EP / (EP + VP) = EP /P'
- Hoeveel van de positieve resultaten zijn ook echt zieke individuen.
- Negative Predictive Value (NPV) = EN / (EN + VN) = EN / N'
- Hoeveel van de negatieve resultaten zijn ook echt gezonde individuen.
- False Discovery Rate (FDR) = VP / (EP + VP) = VP / P'
- Hoeveel van de positieve resultaten zijn eigenlijk gezonde individuen.
Aangezien de prevalentie van een ziekte binnen de populatie van dieren die we in de praktijk tegenkomen vrij laag is, heeft de minste vals positieve meting een gewichtige invloed op de PPV. Voor de meeste testen zal PPV dan ook laag zijn en NPV hoog. Anders gezegd: in zijn algemeenheid is een negatief resultaat een betrouwbaar criterium om een ziekte uit te sluiten, maar een positief resultaat dient bevestigd te worden. Hetzij door toegevoegde bewijskracht te vinden bij andere afwijkende parameters of door de test eenvoudigweg te herhalen.
Conclusie
Juiste populatie gebaseerde RI zijn en blijven belangrijke informatie verstrekt door het laboratorium. De toepassing ervan tijdens de interpretatie van een labo-onderzoek is echter meer dan het vergelijken van de harde cijfers maar vergt ook kennis en inschatting van alle factoren die een meetresultaat kunnen beïnvloeden. In onze Wikilab labogids trachten we zoveel mogelijk van deze factoren te duiden.
Volgens welke methode ze ook opgesteld werden RI zijn steeds het product van statistiek. "Geen enkel RI is volledig juist of fout".[10] RI worden opgesteld rond de centrale 95% van de referentiepopulatie. 5% perfect gezonde dieren vallen dus per definitie buiten de RI-grenzen. Nemen we een routine labo-onderzoek waarin 20 parameters gemeten worden, kunnen we berekenen dat de kans dat er bij een perfect gezond individu minstens 1 waarde afwijkt tov het RI, 64% bedraagt (1 - (520/10020)) of slechts 1 op 3 dat alles inderdaad binnen de RI's valt.
Als we met der tijd meer kennis verwerven rond intra-individuele biologische variabiliteit kunnen ook andere meer geïndivualiseerde benaderingen gebruikt worden zoals RCV om een meetwaarde te kaderen.
Hoe dan ook blijft de boodschap dat men labo-bevindingen steeds dient te toetsen aan de kliniek, labo-onderzoek kan nooit het basis klinisch onderzoek vervangen..
Referenties
- ↑ Walton: Subject-based reference values: biological variation, individuality, and reference change values. Vet Clin Pathol 2012;41:175-81. PMID: 22390475. DOI.
- ↑ 2,0 2,1 Ricós et al.: Within-subject biological variation in disease: collated data and clinical consequences. Ann. Clin. Biochem. 2007;44:343-52. PMID: 17594781. DOI.
- ↑ Ruaux et al.: Estimates of biological variation in routinely measured biochemical analytes in clinically healthy dogs. Vet Clin Pathol 2012;41:541-7. PMID: 23025456. DOI.
- ↑ Walton: "Biological variability of C-reactive protein and specific canine pancreatic lipase immunoreactivity in apparently healthy dogs". J. Vet. Intern. Med. 2012;26:1; author reply 2. PMID: 22233342. DOI.
- ↑ Jensen et al.: The long-term biological variability of fasting plasma glucose and serum fructosamine in healthy Beagle dogs. Vet. Res. Commun. 1999;23:73-80. PMID: 10359151.
- ↑ Kellihan et al.: Weekly variability of plasma and serum NT-proBNP measurements in normal dogs. J Vet Cardiol 2009;11 Suppl 1:S93-7. PMID: 19395335. DOI.
- ↑ Cotlove et al.: Biological and analytic components of variation in long-term studies of serum constituents in normal subjects. 3. Physiological and medical implications. Clin. Chem. 1970;16:1028-32. PMID: 5481563.
- ↑ 8,0 8,1 Reference Intervals, M. Kjelgaard-Hanssen, A.L. Jensen in Clinical Biochemistry of Domestic Animals; 6th Ed, 2008; Jiro Jerry Kaneko, John W. Harvey, Michael L. Bruss; ISBN 9780123704917
- ↑ 9,0 9,1 Geffré et al.: Reference values: a review. Vet Clin Pathol 2009;38:288-98. PMID: 19737162. DOI.
- ↑ 10,0 10,1 Katayev et al.: Establishing reference intervals for clinical laboratory test results: is there a better way?. Am. J. Clin. Pathol. 2010;133:180-6. PMID: 20093226. DOI.
- ↑ Fraser & Harris: Generation and application of data on biological variation in clinical chemistry. Crit Rev Clin Lab Sci 1989;27:409-37. PMID: 2679660. DOI.
- ↑ Petersen et al.: The index of individuality is often a misinterpreted quantity characteristic. Clin. Chem. Lab. Med. 1999;37:655-61. PMID: 10475074. DOI.
- ↑ Iglesias et al.: Power function of the reference change value in relation to cut-off points, reference intervals and index of individuality. Clin. Chem. Lab. Med. 2005;43:441-8. PMID: 15899662. DOI.
- ↑ Cooper et al.: Collective opinion paper on findings of the 2010 convocation of experts on laboratory quality. Clin. Chem. Lab. Med. 2011;49:793-802. PMID: 21366504. DOI.